What will it take to further increase the broad practical utility of computation? Few if any technical challenges loom larger than that of radically improving our ability to find – with lower latency and energy consumption – better solutions to hard optimization problems. Optimization problems lie at the heart of application areas such as transportation and logistics; utilities management and climate change; public policy and social justice; engineering design of circuits, structures, molecules, and medicines; pharmaceutical trials; machine learning, artificial intelligence, and computer vision. In these modern contexts, we find optimization tasks integrated within complex heterogeneous workflows that foreground nontraditional factors such as energy/power constraints, price-performance tradeoffs, uncertain models and data, transparency requirements, human factors, and cloud computing. At the same time, the hardware substrate of computing is evolving with the onset of formidable obstacles to further improvements in conventional CMOS technology, and the introduction of novel materials and integrated photonics to minimize energy dissipation and facilitate massive data transport. High-profile industrial efforts to demonstrate quantum computers have likewise reignited broad interest in special- purpose information processing architectures, including optimizers such as the D-Wave quantum annealers. Forward-looking research in optimization thus cannot focus on conventional algorithms or code development alone.

The NSF Expedition in Coherent Ising Machines is a 5-year, $10M project focusing on the development and assessment of new classes of specialized computing architectures for optimization. Our project team comprises research groups specializing in mathematical analysis of optimization, cutting-edge nanophotonic and quantum optical technologies, simulation and benchmarking of unconventional computing architectures, and practical applications of machine learning. We were brought together by our complementary engagements with testing and analysis of Coherent Ising Machines (What is a Coherent Ising Machine?) through new collaborative interactions we are pursuing an expansive agenda in physics-based optimization.

Our project agenda encompasses five major areas of emphasis:

• Fundamentals – How can physical dynamics beyond the scope of conventional digital electronics provide novel foundations for solving hard optimization problems? What performance advantages can unconventional approaches offer, and what obstacles must be overcome to realize them? Do unconventional models of computing facilitate new approaches to analyzing what makes some optimization instances much harder than others?

• Generalizations – We take the Coherent Ising Machine (CIM) as our starting point and reference, but many generalizations of this architecture are now being explored. What are the operational bottlenecks of canonical CIM, and can CIM be modified to circumvent them? How can CIM-type architectures be generalized to solve optimization problems with non-binary variables, with higher- than-quadratic cost functions, and/or natively incorporating constraints? Are there potential quantum advantages in CIM-type architectures?

• Applications – What practical applications can make use of the CIM and its generalizations? How can real-world problems be mapped into the quadratic-binary-unconstrained-optimization framework of canonical CIM, and what computational overhead is incurred in doing so? What concrete performance thresholds do practical applications set for CIM hardware to have a strong use case? What feasible generalizations of canonical CIM would open important new applications?

• Benchmarking – How can unconventional optimization architectures such as CIMs and quantum annealers be compared with conventional algorithms, and with each other, in a principled way? How should scaling be defined for computational problems for which heuristic algorithms exhibit performance complementarity? Can we develop benchmarking testbeds that capture the statistics of real-world optimization problems?

• Broadening Participation in Computing – We are partnering with the Stanford Center for Human- Centered Artificial Intelligence, Stanford Graduate School of Education, and a local non-profit organization to study factors affecting computer science identity and career track persistence among students from historically minoritized backgrounds. Our senior personnel and their research groups are based at Stanford University, California Institute of Technology, Cornell University, NTT Research, and University Space Research Association/NASA Ames.

Our senior personnel and their research groups are based at Stanford University, California Institute of Technology, Cornell University, NTT Research, and University Space Research Association/NASA Ames.

What is a Coherent Ising Machine?

The CIM architecture cannot be viewed simply as a neural network or an annealer working on principles of thermalization or the quantum adiabatic theorem. It is inspired by all of these predecessors, however, and is designed to build on their strengths while avoiding some key weaknesses. Its operating principle is fundamentally different from that of previous hardware approaches and of all current algorithms for performing optimization on classical computers.

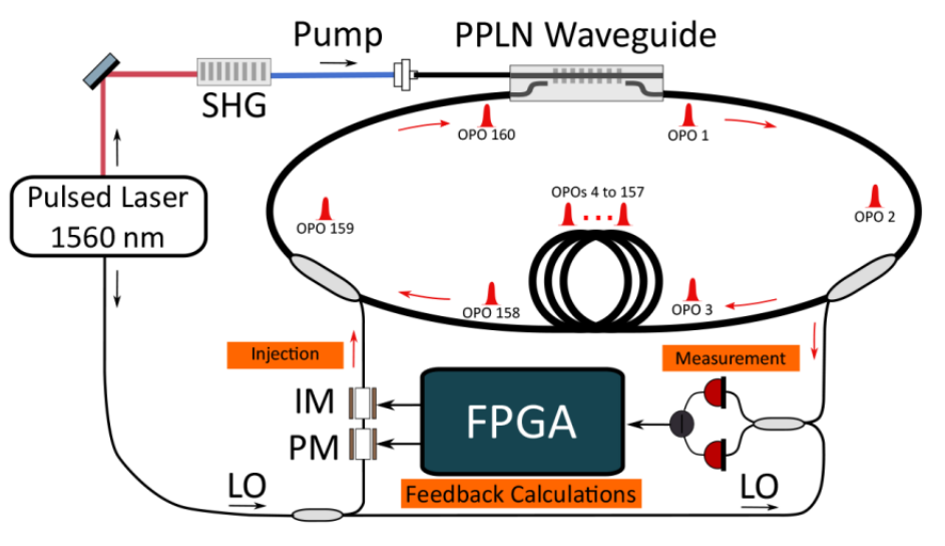
A conceptually straightforward realization of the CIM architecture can be constructed as an optically pumped network of coupled degenerate optical parametric oscillators (DOPOs). The coupling coefficients implemented among the constitutent DOPOs encodes a specific Ising Hamiltonian. The phase portrait of the network — a driven dissipative dynamical system — undergoes bifurcations as the pump strength is increased from zero. Theoretically, the equilibrium states of an ideal CIM realization just above its lowest-lying bifurcation coincide with ground states of the Ising Hamiltonian encoded by the coupling coefficients among its constituent DOPOs. While we do not yet fully understand the physical dynamics of the “search process” by which the network re-equilibrates when a bifurcation point is crossed, and many questions remain regarding the quantitative impact of implementation errors and exogenous noise, currently laboratory implementations achieve impressive computational performance.

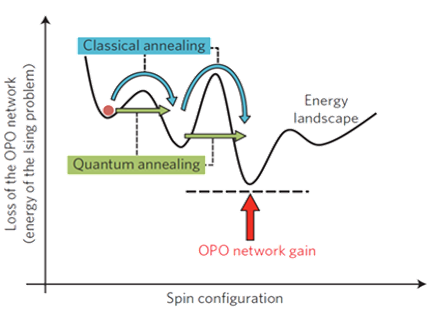
Recent studies have investigated the computational performance of current prototypes and near-term-realizable variants of CIM, relative to conventional computing approaches and emerging quantum platforms. Such results are motivating intensive investigations of CIM theory and implementations by a growing community of researchers, which held its first international conference in March, 2019 with plans for a follow-up meeting in July, 2020 (details coming soon).

See Also

• P. L. McMahon, To Crack the Toughest Optimization Problems, Just Add Lasers (2018)
• Y. Yamamoto, Coherent Ising machines — optical neural networks operating at the quantum limit (2017)
• A. Lucas, Ising formulation of many NP problems (2014)

References

1. Z. Wang, A. Marandi, K. Wen, R. L. Byer and Y. Yamamoto, Coherent Ising machine based on degenerate optical parametric oscillators, Phys. Rev. A 88, 063853 (2013).
2. Y. Haribara, S. Utsunomiya and Y. Yamamoto, Computational Principle and Performance Evaluation of Coherent Ising Machine Based on Degenerate Optical Parametric Oscillator Network, Entropy 18, 151 (2016).
3. A. Marandi, Z. Wang, K. Takata, R. L. Byer and Y. Yamamoto, Network of time-multiplexed optical parametric oscillators as a coherent Ising machine, Nature Photonics 8, 937 (2014).
4. T. Leleu, Y. Yamamoto, S. Utsunomiya and K. Aihara, Combinatorial optimization using dynamical phase transitions in driven-dissipative systems, Phys. Rev. E 95, 022118 (2017).
5. R Hamerly et al., Experimental investigation of performance differences between coherent Ising machines and a quantum annealer, Science Advances 5, eaau0823 (2019).
6. P. L. McMahon et al., A fully programmable 100-spin coherent Ising machine with all-to-all connections, Science 354, 614 (2016).
7. T. Leleu, Y. Yamamoto, P. L. McMahon and K. Aihara, Destabilization of Local Minima in Analog Spin Systems by Correction of Amplitude Heterogeneity, Phys. Rev. Lett. 122, 040607 (2019).